Optimizing Algorithm to Determine Primality of Number Using Ruby

A few months ago I stumbled upon an interesting problem on Projecteuler, which hosts “challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems”.

The problem was as follows:

By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13, we can see that the 6th prime is 13. What is the 10,001st prime number?

Because Eulerproject.net is supposed to be used as a learning tool, I am going to follow the original author’s wishes and not publish direct solutions to questions online. But we can instead explore the core question being asked in this problem, how do you determine whether or not a number is prime?

Brute Force

Determining whether a number is prime or not appears to be relatively easy as n stays relatively small. Let’s take 5 for example. We as human beings determine if a number is prime by dividing n by every integer between itself and 1. For 5, we would say

5/5 is an integer.

5/4 is not an integer.

5/3 is not an integer.

5/2 is not an integer.

5/1 is an integer.

By knowing the definition of a prime number we can determine that because 5 is a prime number because it is only evenly divisible by itself and 1. This is a feasible method while n stays relatively small. But how long would it take you to tell me whether or not 472,882,027 is prime using this method? (spoiler:A really long time and yes it’s prime.)

Well luckily my computer is a billion times smarter than me (RIP jobs) so let’s go ahead and make a program in ruby that determines whether a number is prime in the same way a human brain would. We can take advantage of the fact my CPU can perform computations a lot faster than a human brain can.

1
2
3
4
5
6
7
8
9
10
11
12
13

def is_prime?(n)
  #these guys don't play by the rules
  if n == 0 || n == 1
    return true
  end
  array_of_factors = []
  for i in (1..n)
    if n % i == 0
      array_of_factors << i
    end
  end
  return array_of_factors.length == 2 #if there are only 2 factors, it must be prime
end

And let’s go ahead and add a way to track how long this thing takes to run. I’m using a latest generation quad-core I7, it should blaze through this no problem! We’re going to be using Ruby’s standard Benchmark library to time our program’s execution.

1
2
3
4
5

n = 11
time = Benchmark.realtime do
  puts "#{n} is #{is_prime?(11)}."
end
puts "Time elapsed #{time*1000} milliseconds."

Console:

1
2

11 is prime.
Time elapsed 0.03200001083314419 milliseconds.

Cool! This means our program can determine that 11 is a prime number in just .032 Milliseconds. Let’s try larger values of n to see how that affects the execution time.

When n = 113.

Console:

1
2

113 is prime.
Time elapsed 0.04499999340623617 milliseconds.

When n = 1000.

Console:

1
2

1000 is not prime.
Time elapsed 0.11299998732283711 milliseconds.

When n = 10000.

Console:

1
2

10000 is not prime.
Time elapsed 0.7440000190399587 milliseconds.

When n = 100000.

Console:

1
2

100000 is not prime.
Time elapsed 6.9629999925382435 milliseconds.

When n = 1000000.

Console:

1
2

1000000 is not prime.
Time elapsed 68.42699996195734 milliseconds.

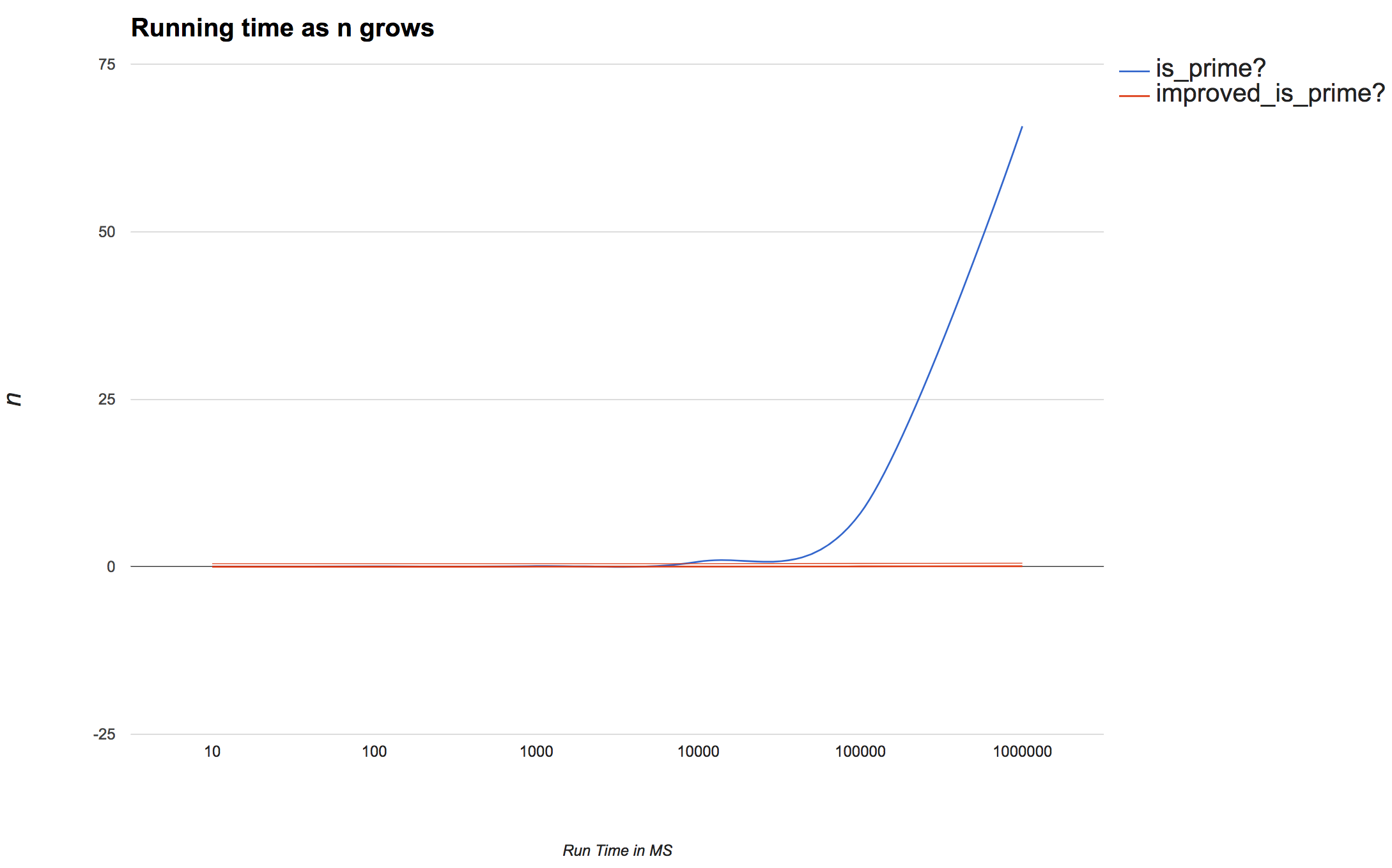
Well this isn’t looking good…

It seems that as the size of our n grows, as does the execution time of our program. Determining whether 1,000,000 is prime takes about ten times longer than determining whether or not 100,000 is prime. We can see now that our human method for determining whether a number is prime or not is not going to be feasible when n gets to a certain size. Determining whether 1,000,300,017 was prime or not would take over 60 seconds to execute, which while slow is still a reasonable amount of time to wait for an answer. But if I were to want to check whether 1,000,000,030,117 was prime or not we’d have to wait over 16 hours for an answer. Fine, this is still technically a feasible amount of time to wait thanks to the invention of Netflix, but what happens when we want to see if

1,000,000,003,020,217 is prime or not?

Optimizing our algorithm:

We need to take advantage of certain mathematical properties of prime numbers in order to speed up the execution time of our program. If we look at our method for determining whether a number is prime or not, we can see we are doing some unnecessary calculations. A number n is prime if the only factor from 1 to the ceiling of sqrt(n) + 1 is 1, yet we check whether or not n is divisible by the ceiling of sqrt(n) + 1….n in our method #is_prime? . Let’s change our algorithm so it only checks for factors from 1 to sqrt(n).ceiling + 1 and see how that affects the running time.

We’ll write a new method called #improved_is_prime? :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def improved_is_prime?(n)
  #these guys don't play by the rules
  if n == 0 || n == 1
    return "prime"
  end
  array_of_factors = []
  for i in (1..Math.sqrt(n).ceil + 1)
    if n % i == 0
      array_of_factors << i
    end
  end
  if array_of_factors.length == 2
    return "prime"
else
    return "not prime"
  end
end

The only thing that changed from the original method we wrote is the range of our for loop. We now only check whether numbers 1 to sqrt(n).ceiling + 1 are factors, let’s take a look at how that affected the running time.

When n = 10.

Console:

1
2
3
4

10 is not prime.
Our original method took 0.037999998312443495 milliseconds.
10 is not prime.
Our improved method took 0.010000017937272787 milliseconds.

When n = 100.

Console:

1
2
3
4

100 is not prime.
Our original method took 0.04499999340623617 milliseconds.
100 is not prime.
Our improved method took 0.010999967344105244 milliseconds.

When n = 1000.

Console:

1
2
3
4

1000 is not prime.
Our original method took 0.10499998461455107 milliseconds.
1000 is not prime.
Our improved method took 0.011999974958598614 milliseconds.

When n = 10000.

Console:

1
2
3
4

10000 is not prime.
Our original method took 0.7489999989047647 milliseconds.
10000 is not prime.
Our improved method took 0.018000020645558834 milliseconds.

When n = 100000.

Console:

1
2
3
4

100000 is not prime.
Our original method took 7.978999987244606 milliseconds.
100000 is not prime.
Our improved method took 0.04600000102072954 milliseconds.

When n = 1000000.

Console:

1
2
3
4

1000000 is not prime.
Our original method took 65.731999988202 milliseconds.
1000000 is not prime.
Our improved method took 0.0819999841041863 milliseconds.

As you can see this slight modification to our method drastically improves the running time of our program, and the execution time is no longer directly related to the size of n. Before we had to perform a million calculations in order to determine whether or not 1,000,000 was prime or not, but our new method only needs to perform sqrt(1,000,000) + 1 or 1,001 calculations in order to determine the exact same thing.

Let’s go ahead and see if our improved method can answer our original question, is 472,882,027 a prime number?, in a reasonable amount of time.

1
2
3
4
5
6
7
8
9
10

n = 472882027
time = Benchmark.realtime do
  puts "#{n} is #{is_prime?(n)}."
end
puts "Our original method took #{time*1000} milliseconds."

time = Benchmark.realtime do
  puts "#{n} is #{improved_is_prime?(n)}."
end
puts "Our improved method took #{time*1000} milliseconds."

Console:

1
2
3
4

472882027 is prime.
Our original method took 31142.99600000959 milliseconds.
472882027 is prime.
Our improved method took 1.352999999653548 milliseconds.

As the size of n grows, the more our optimization improves the running time of the program. With this slight change to our original method we have made the process of determining whether or not 472,882,027 is prime over 23,000 times faster, and created a way to determine whether or not even larger values of n are prime in a reasonable amount of time.

Conclusions:

Exploring this topic reveals an important aspect of Computer Science. Brute force alone cannot solve all of the world’s problems, and it is up to us as computer scientists to come up with creative solutions in order to overcome these obstacles. Sadly, our previous solution of MOAR TRANSISTORS isn’t going to cut it unless a serious revolution occurs in the design of the modern day CPU. Plenty of problems like prime numbers still exist today, except their “improved” solutions have yet to be found (or may never be found depending on who you’re asking).

In future blog posts we are going to explore ways we can make this algorithm even faster, talk about some of these problems that have yet to be optimized, and dive into one of the greatest unsolved problems in mathematics, P vs. NP, so stay tuned!