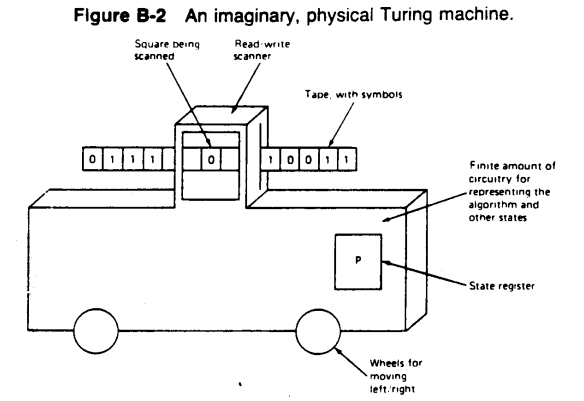
A turing machine is an abstract model of computation used to formally define what it means for a function to be computable. As you will see shortly the model of a turing machine is simple, but given any computer algorithm, a Turing machine can be created that is capable of simulating that alorithm’s logic.
It consists of:
An infinitely long tape which serves as the memory for the machine. The tape consists of squares which are usually blank at the start and can be written with symbols.
A read/write “head” which is positioned over one of the squares on the tape.
The head is capable of three basic operations:
- Reading the symbol on the tape
- Editing the symbol on the tape by writing a new symbol or erasing it.
- Moving the tape left or right by one square so that the turing machine can read or edit the neighbouring symbols.
That’s it!
A turing machine is given a set of instructions that tell it what actions to perform based on the given input on the tape.
The action that a Turing Machine is going to take is determined by the current state of the machine, the symbol in the cell currently being scanned by the read/write head and a table of transition rules. These transition rules can be thought of as “programs” that the Turing Machine then runs.
Here’s what some simple instructions look like, taken from a rasberry pi overview published by University of Cambridge:

We could write these instructions as such:
1 2 3 4 5 6 7 8 | |
This example is pretty boring though, what if something was already written on the tape?
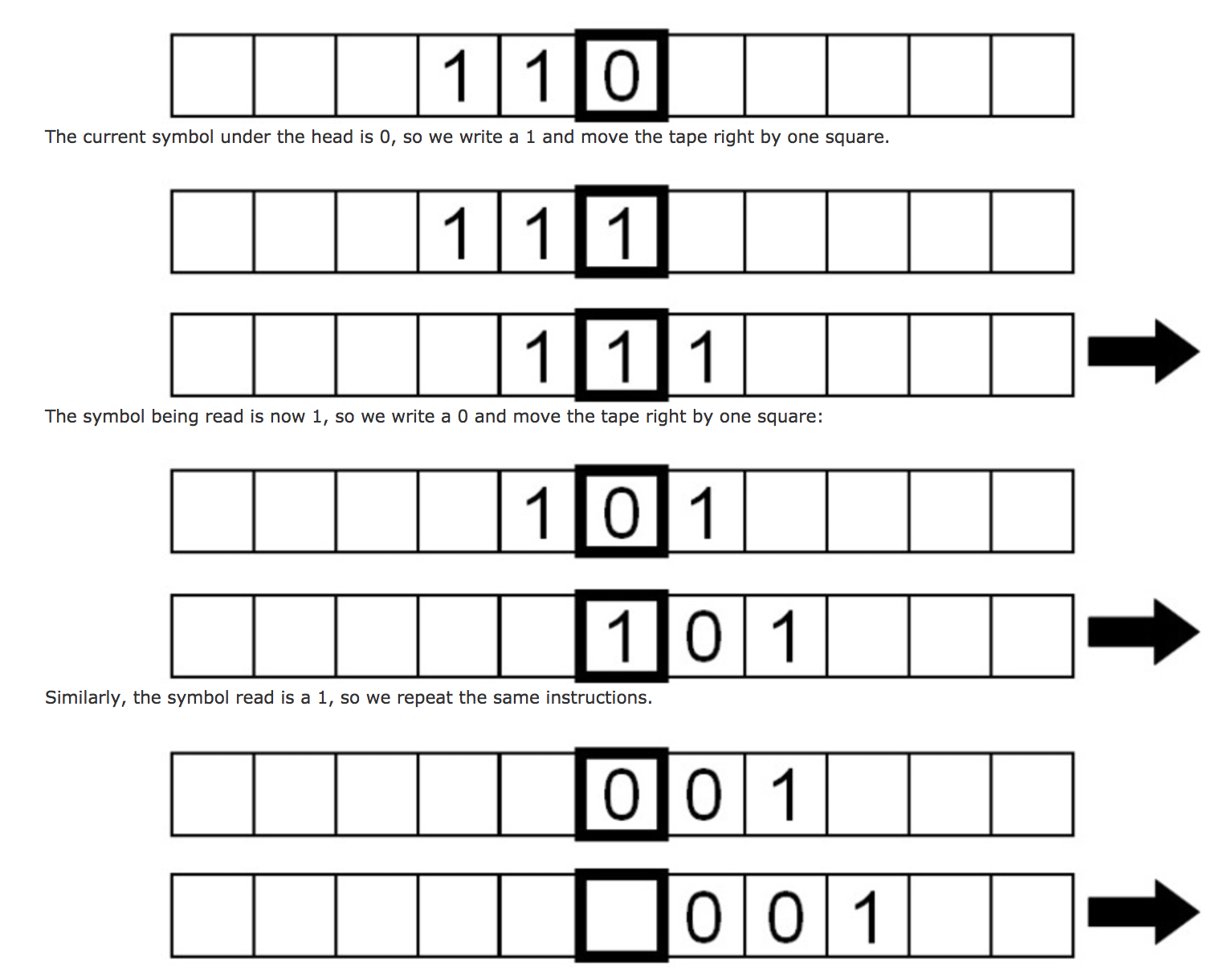
Here’s a program that creates the binary inverse of a binary number written on the tape. (The binary inverse of 110 would be 001).
1 2 3 4 5 6 7 8 9 10 11 12 | |
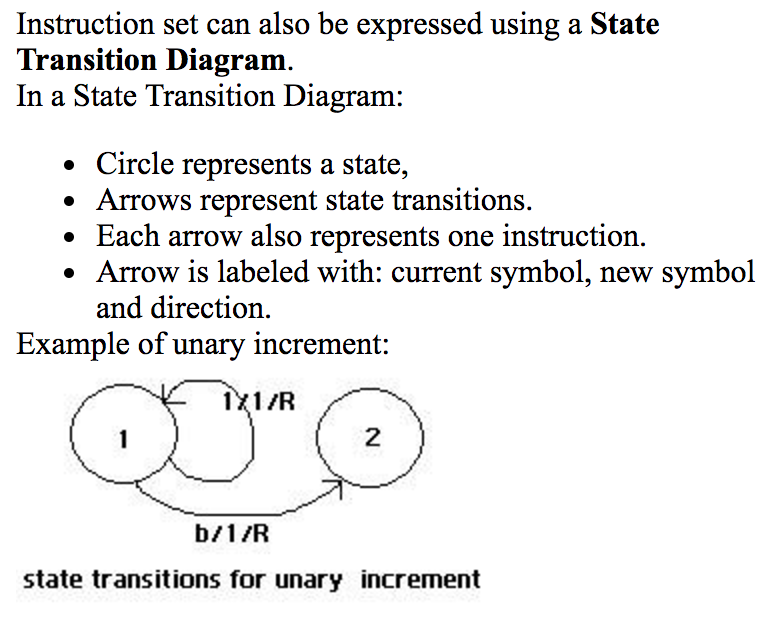
We’re writing some pretty sketchy pseudo code to represent the instructions given to a Turing Machine. Usually, instructions are represented using state transition diagrams. Here’s an example of a set of instructions that adds one to a unary representation of a number. It also has a good explanation of how a state transition diagram represents the different instructions:
Now let’s see that program run in real time:

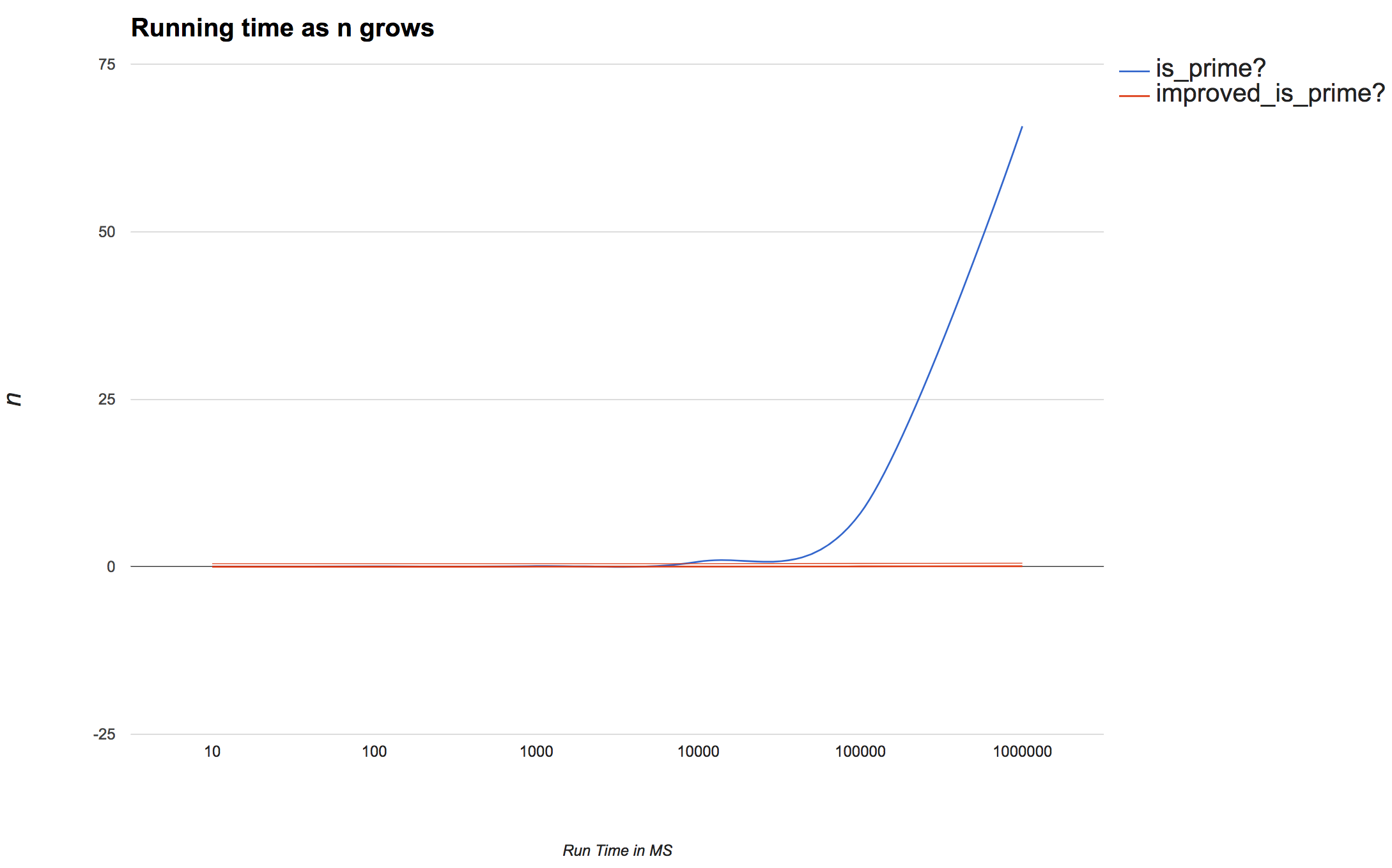
Why have I never seen one of these Turing Machine’s before?
Well, a Turing Machine is really just a hypothetical machine used as a model to prove certain limits on mechanical computation. But, it is possible to build one if you really wanted.
Now that we understand what a Turing Machine, let’s take a look at…
The Halting Problem
In computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running or continue to run forever. https://en.wikipedia.org/wiki/Halting_problem
In other words, can you write a program that given some computer and some other program as parameters, could tell you whether the given program would run forever on that computer, or at some point would stop and give you an answer.
Hm… it’s starting to make sense why all these famous computer scientists look like dead heads.
Well, let’s try and prove this.
First, we’ll assume that we DO have some program that can achieve this feat. We can give it a program and a computer, and it will tell us whether that program will run forever or not. We’ll call it “Does it halt?”, represented by the weird diamond boxy thing below and trust that it returns either a true or false value.

If I gave this weird diamond box thingy this program in BASIC as a parameter:
1 2 | |

In other words, if we represent it as a function:
1 2 3 | |
Alright, this is where things get weird…
Now, imagine we made this little magical “Does It Halt?” program a piece of a bigger program? Let’s make it that if the “Does It Halt?” algorithm returns true, then we make our new program loop forever. But if it returns false, then we’ll halt (or end) our new program, which we will name “Program X”.

Program X
Now, here’s the kicker. What would happen if we fed Program X into itself? In other words, what if we ran Program X and gave it Program X as the parameter?

So, now if the program doesn’t halt, then it halts. But if it DOES halt, then it doesn’t halt. What the hell?
What we have done is created a paradox, and in doing so proven that the answer to the question is undecidable, or it is neither true nor false. We can then conclude that our assumption that there exists a program which can answer the question of “Does It Halt?” must also be false.
We can then conclude that given a program and a computer, it is not possible to create a program that can tell you whether that program on that given machine will run forever, or eventually give you an answer.
Sources:
- http://faculty.otterbein.edu/PSanderson/csc150/notes/chapter11.html
- https://plato.stanford.edu/entries/turing-machine/
- https://www.cl.cam.ac.uk/projects/raspberrypi/tutorials/turing-machine/one.html
- http://danielschlegel.org/teaching/111/lecture4.html



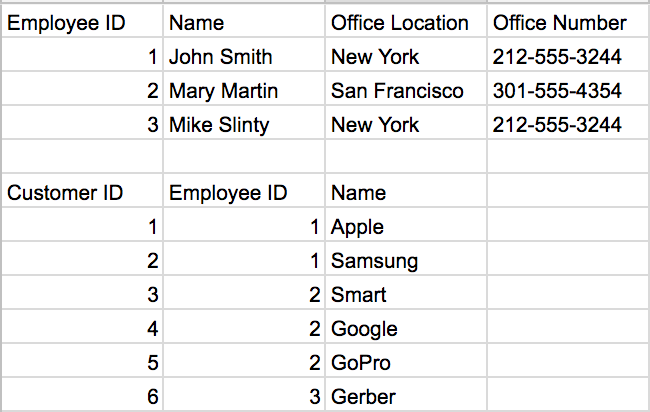
 Someone should call our San Francisco office to let them know about Mary. We’ll just look up their number from our database and…
Oh no! When we delete the row pertaining to “Mary Martin”, we also deleted our Office Number for the San Francisco office. A normalized database would store these Office Locations and their respective numbers in such a way that when we delete an employee that works at that location, we still have access to that location’s information, even if there are not currently any employees working there.
Someone should call our San Francisco office to let them know about Mary. We’ll just look up their number from our database and…
Oh no! When we delete the row pertaining to “Mary Martin”, we also deleted our Office Number for the San Francisco office. A normalized database would store these Office Locations and their respective numbers in such a way that when we delete an employee that works at that location, we still have access to that location’s information, even if there are not currently any employees working there.
 As the number of customers each employee has grows, our database has to grow horizontally in order to store these new customers. This is not what we want.
Furthermore, how would we query our database for a specific customer using SQL? We’d have to set up a query like this:
As the number of customers each employee has grows, our database has to grow horizontally in order to store these new customers. This is not what we want.
Furthermore, how would we query our database for a specific customer using SQL? We’d have to set up a query like this:
 We have now almost completely eliminated redundancy. Remember our update anomaly we ran into before? Now if we needed to update the office number for our San Francisco office, we only need to make one update to our table, while before we would have had to update it everywhere it appeared in the 1NF of the customer table.
We have now almost completely eliminated redundancy. Remember our update anomaly we ran into before? Now if we needed to update the office number for our San Francisco office, we only need to make one update to our table, while before we would have had to update it everywhere it appeared in the 1NF of the customer table.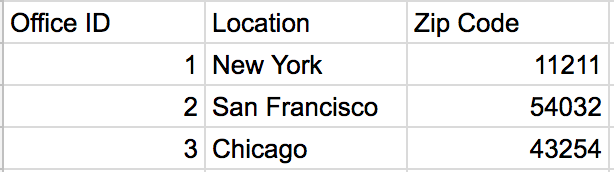 Let PK = Office ID, A = Zip code and B = Office Location.
A, the zip code, relies on the primary key because the zip code is a representation of where that Office is located. B, the office location, relies on A because the zip code points to the city in which the office is located. Because of this, A relies on the Primary Key through B.
Let PK = Office ID, A = Zip code and B = Office Location.
A, the zip code, relies on the primary key because the zip code is a representation of where that Office is located. B, the office location, relies on A because the zip code points to the city in which the office is located. Because of this, A relies on the Primary Key through B.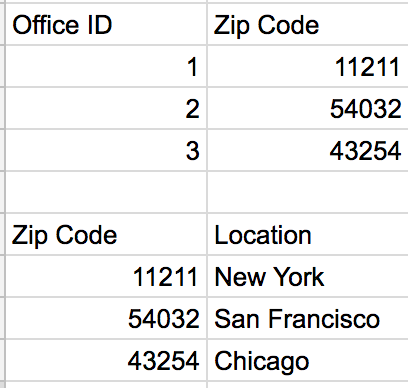
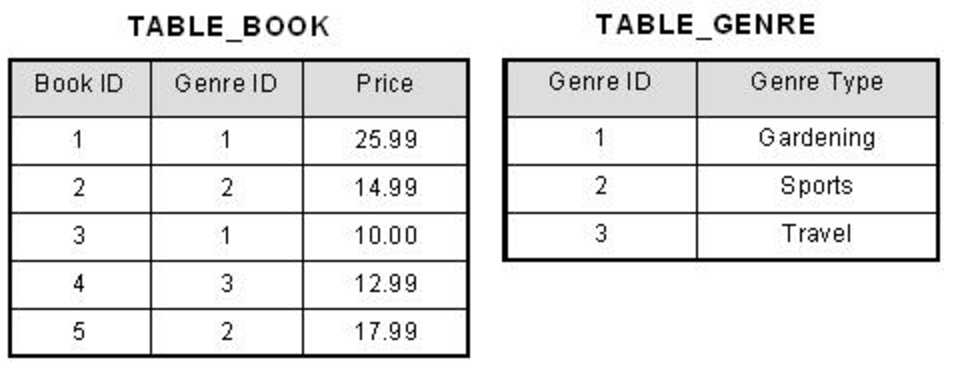
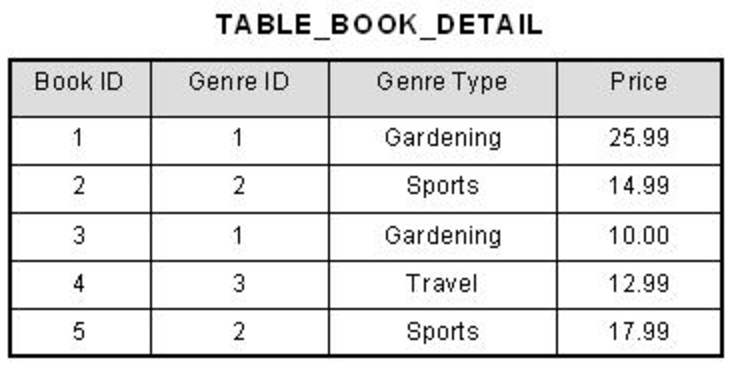 Our original table, “TABLE_BOOK_DETAIL” has both a “Genre ID” and “Genre Type” column. Book ID, which we will refer to as the primary key, is used to determine the Genre ID. Then the Genre ID is used to determine the Genre Type column. Because of this, we can see that the Primary Key determines the Genre Type through Genre ID. This violates our second rule of 3NF, and thus we need to separate out Genre Type into it’s own table which is referenced by the Genre ID.
Our original table, “TABLE_BOOK_DETAIL” has both a “Genre ID” and “Genre Type” column. Book ID, which we will refer to as the primary key, is used to determine the Genre ID. Then the Genre ID is used to determine the Genre Type column. Because of this, we can see that the Primary Key determines the Genre Type through Genre ID. This violates our second rule of 3NF, and thus we need to separate out Genre Type into it’s own table which is referenced by the Genre ID.